今回は、音声信号をいろいろ分析・加工するための方法として、STFTの実験をしてみます。
STFTについて
STFTとは
STFTとは、Short-Time Fourier Transform または Short-Term Fourier Transoform=短時間フーリエ変換のことです。フーリエ変換は、非常に大雑把に言えば『対象の信号に各周波数成分がどの程度含まれているか』を分析するものでした。STFT は通常のフーリエ変換とは異なり、一度に信号全体を見るのではなく小さな窓を通して狭い範囲ずつ見ていくことで、『ある時刻に、ある周波数成分がどのくらいの量だけ含まれているか』を分析することができます。
数式で表すと、
\[\Large S(t,\omega)=\int^\infty_{-\infty}x(\tau)w(\tau-t)e^{-i\omega\tau}d\tau\]
なる関数\(S(t,\omega)\)を求める操作がSTFTです。
ただし、
\(x(t)\) は対象の信号を表しています。
\(w(t)\) は『窓関数』と呼ばれています。\(t=0\) 付近を最大値1をとり、\(t\) が0から離れるほど値が0に近づく山型の関数で、\(x(t)\) から \(t=\tau\) 付近を切り取る役割を持ちます。
\(t\)は時刻、\(\omega\) は各振動数を表しています。\(S(t,\omega)\) は複素数の値をもち、時刻 \(t\) における角振動数 \(\omega\) の成分の振幅(絶対値)および位相(偏角)を表しています。
PythonでSTFT
Pythonでは、scipy.signal モジュールの stft() メソッドで簡単にSTFTを行うことができます。
(scipyのver.0.19.0以降で使うことができます。これより古いものがインストールされている場合はバージョンアップして下さい)
基本的な使い方は以下の通りです。
f, t, spectrum = stft(src, fs, window, nperseg)
引数
引数として、以下を指定します(他にもありますが、今回はデフォルト値で使用しています)
src
サンプリングデータのリスト(リスト型、numpy.ndarray型など)。必須です。
fs
サンプリング周波数。デフォルト値は1.0です。
window
窓関数の形状です。通常は省略で良いでしょう。
nperseg
セグメントの大きさ(一度に切り取るサンプリングデータ数)です。デフォルト値は256です。
返却値
返却値は以下の通りです。
f
周波数のリスト(numpy.ndarray)。下の spectrum の項の f1, f2, …, fn を表します。
(分析できる周波数の間隔はサンプリング周波数 fs とセグメントの大きさ nperseg によって決まります)
t
時刻のリスト(numpy.ndarray)。下の spectrum の項の t1, t2, …, tn を表します。
分析できる時間の間隔はサンプリング周波数 fs とセグメントの大きさ nperseg によって決まります。
spectrum
変換結果。2次元の配列(numpy.ndarray)で、
[ [S(t1,f1), S(t1,f2), …, S(t1, fn) ],
[S(t2,f1), S(t2,f2), …, S(t2, fn) ],
…
[S(tn,f1), S(tn,f2), …, S(tn, fn) ] ]
という型式になっています。
ただし S(t, f) は、時刻 t における周波数 f の成分の振幅と位相を複素数で表した値です。
試してみる
それでは、実際に scipy.signal.stft() を使って音声信号を分析してみましょう。
サンプルプログラム
まず、実験に使うソースコードは以下の通りです。
import numpy
import soundfile
from scipy.signal import stft
from matplotlib import pyplot
src, samplingfreq = soundfile.read("input.wav")
f, t, spectrum = stft(src, fs=samplingfreq, nperseg=256)
pyplot.pcolormesh(t,f,numpy.abs(spectrum))
pyplot.show()ソースコード解説
冒頭部
import numpy
import soundfile
from scipy.signal import stft
from matplotlib import pyplotいつも通り必要なモジュールをimportしています。
soundfile は初登場です。これはwavファイルの読み書きのためのモジュールです。
いままでwavファイルの読み込みには独自のモジュールを使っていましたが(いくつか前の記事でwavファイルのフォーマットの勉強のためにつくったのです)、思ったより音声絡みの記事が増えてきて、それぞれの記事だけ読んで試したい人もいるかもしれないので有名なモジュールを使うことにします。
scipy.signal モジュールの stft が今回のキモです。
matplotlib モジュールの pyplot は、分析結果の表示のために使用します。
ファイルの読み込み
src, samplingfreq = soundfile.read("input.wav")wavファイルの読み込みには、soundfileモジュールの read() メソッドを使用します。
使い方は以下の通りです。
data, samplingfreq = soundfile.read(path)
引数
path
読み込みたいwavファイルのパスを指定します。
返却値
data
読み込んだサンプリング値のリスト(numpy.ndarray)が返されます。モノラルの場合は1次元リスト、ステレオの場合は2次元リストになります。
samplingfreq
サンプリング周波数が返されます。
STFT
f, t, spectrum = stft(src, fs=samplingfreq, nperseg=256)STFT処理はたった一行です。stft() メソッドについては上で説明しているので省略します。
結果表示
pyplot.pcolormesh(t, f, numpy.abs(spectrum))
pyplot.show()結果表示には matplotlib.pyplot.pcolormesh() メソッドを使用しています。これはパラメータが2個ある関数 f(x,y) を表示するためのもので、x,y 平面上に f(x,y) の値を色で表現します。
matplotlib.pyplot.pcolormesh(x, y, f)
引数
x
横軸のデータ列(リスト)を与えます。
y
縦軸のデータ列(リスト)を与えます。
f
f(x,y) の値を2次元のリストで与えます。
返却値
matplotlib.collections.QuadMesh型のオブジェクトが返却されていますが、グラフをプロットするだけなら使わないので捨ててしまって構いません。
なお、stft() の結果の spectrum は振幅と位相の両方を表現する複素数の2次元リストですが、複素数は pcolormesh() で表示できないので、numpy.abs() で絶対値=振幅のみを取り出して pcolormesh() に与えています。
正弦波を分析
まず、次のような音階で試してみましょう。
サンプリング周波数=8kHz
波形=正弦波
音階(C4=262.6Hz~C5=523.3Hz)
1つの音の長さ=1秒
で試してみましょう。
結果はこのようになります。
横軸が時刻(秒)、縦軸が周波数(Hz)です。下の方に階段状の線が表示されていますが、これが検出された音の成分です。1秒ごとにだんだん周波数(音階)が上がっていく様子がちゃんと判別できます。また、縦軸の目盛り間隔が大雑把なので判りにくいですが、左端は300Hzあたり(本当はC4=262.6Hz)、右端は500Hzあたり(本当はC5=523.3Hz)であることも読み取れます。
矩形波を分析
次に、波形を矩形波に変えて試してみましょう。
サンプリング周波数=8kHz
波形=矩形波
音階(C4=262.6Hz~C5=523.3Hz)
1つの音の長さ=1秒
波形が変わった以外は前のものと同じ条件です。
結果はこのようになります。
一番下の黄緑色の線は正弦波の場合と同じですが、矩形波では上に薄い色でたくさんの階段状の線が表示されます。正弦波と異なり、矩形波には基本周波数の他に3倍・5倍…と奇数倍の周波数の成分が含まれているので、それが表示されているのです。
STFTの注意点
周波数の分解能
では、再び正弦波の音階の分析結果をよく見て見ましょう。時刻0~4秒、周波数0~600Hzの範囲を拡大してみます。
拡大すると、縦軸方向にぼやけたように幅が出てしまっている、つまり周波数があいまいであることがわかります。この例では、音階毎に1つの周波数成分しか持たないので、理想的には、
このようになって欲しいところです。
何故こうなるかは、stft() メソッドの返却値の1つ、f の内容を見ると判ります。
stft() の直後に f の値を表示すると、
[0. 31.25 62.5 93.75 125. 156.25 187.5 218.75 250. 281.25 312.5…]
となっています。これは、周波数の『目盛り』が31.25Hz刻みになっていて、それより細かい違いは判別できないことを表しています。このため、例えばC4=262.6Hzは、近い『目盛り』である250Hzの成分と281.25Hzの成分が少しずつ、のように検出されてしまうのです。
このように、どのくらい周波数の目盛りを細かくできるか、のことを『周波数分解能』といいます。
音階の周波数の差をみると、例えば C4=262.6Hz、D4=293.7Hz で差が31.1Hzしかありません。つまり周波数分解能が31.25Hzでは、ドとレがはっきり判別できないということになりかねず、よろしくありません。
窓の大きさを変える
実は周波数分解能は、サンプリング周波数と窓の大きさ(stft() メソッドの引数 nperseg)によって決まります。サンプリング周波数を \(f_s\) 、窓の大きさを \(n\) とすると、
周波数の目盛りの上限は \(\displaystyle\frac{f_s}{2}\) [Hz]、
周波数の目盛りの刻み幅は \(\displaystyle\frac{f_s}{n}\) [Hz]
となります。つまり、窓の大きさを大きくすれば周波数分解能が高くなる=より細かい目盛りで分析できるようになります。
では試してみましょう。
サンプルプログラムのstft()メソッドの nperseg の値を1024に変更します。
f, t, spectrum = stft(src, fs=samplingfreq, nperseg=1024)結果はこのようになります。
一見して判るように、グラフの線が細く(周波数の目盛りが細かく)なっています。
f の値を調べてみると、
[0. 7.8125 15.625 23.4375 31.25 39.0625 46.875 54.6875 62.5…]
と、7.8125Hz刻みで周波数成分を検出できるようになっています。これならC4=262.6HzとC#4=277.2Hzの差のさらに半分程度なので、半音の違いでもはっきり検出できそうです。
このように、窓の大きさを大きくすればするほど周波数分解能は改善します。たとえば窓の大きさを1秒あたりのサンプリングデータ数=サンプリング周波数と同じにすれば、1Hz刻みでの検出ができるようになります。
時間分解能
では、窓の大きさは大きければ大きいほどよいのかというと、そうではありません。
先ほどのサンプルで、窓の幅をさらに大きく、4096にして試してみましょう。
f, t, spectrum = stft(src, fs=samplingfreq, nperseg=4096)結果はこのようになります。
縦方向の線の幅はさらに細くなっています。つまり周波数を正確に検出できるようになっているのですが、こんどは線が二重になっている部分が出てきました。たとえば時刻1.0~1.2くらいの範囲では、C4の音とD4の音が両方少しずつ出ているかのように表示されています。
何故こうなるかは、stft() メソッドの返却値の1つ、t の内容を見ると判ります。
stft() の直後に t の値を表示すると、
nperseg=256の場合は
[0. 0.016 0.032 0.048 0.064 0.08 0.096 0.112 0.128…]
と、0.016秒刻みになっているのに対して、
nperseg=4096の場合は
[0. 0.256 0.512 0.768 1.024 1.28 1.536 1.792 2.048…]
と、0.256秒刻みになっています。音の周波数が切り替わるタイミングを0.256秒より細かい精度で読み取ることができないのです。
このように、音の周波数の時間変化をどれくらい時間方向に細かく検出できるか、どのくらい時間軸の目盛りを細かくできるかのことを『時間分解能』といいます。
この時間分解能は、音の変化が早い場合には大きな問題になります。ここまでのサンプル音源は1秒に1回しか音が変化してしまいましたが、もっとテンポの速い曲の分析をするとどうなるでしょう?
この音源で試してみましょう。
この音源では、音符1つの長さが0.125秒です。
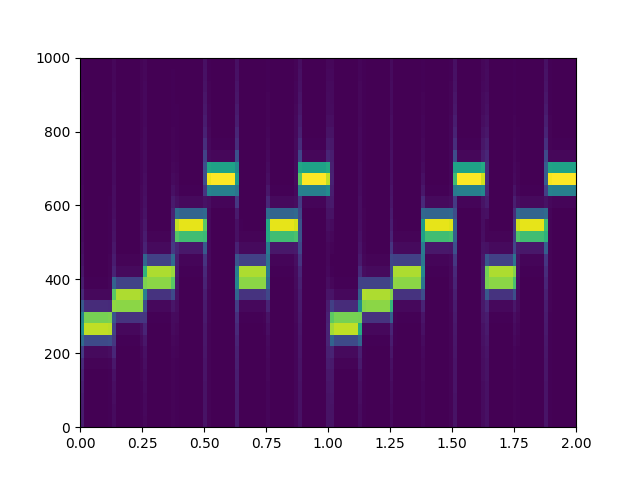
nperseg=256
周波数分解能は悪いものの、時間分解能0.016秒は音符の長さ0.125秒に対して1/8程度と短いため、音程の変化するタイミングは比較的正確に分析できています。
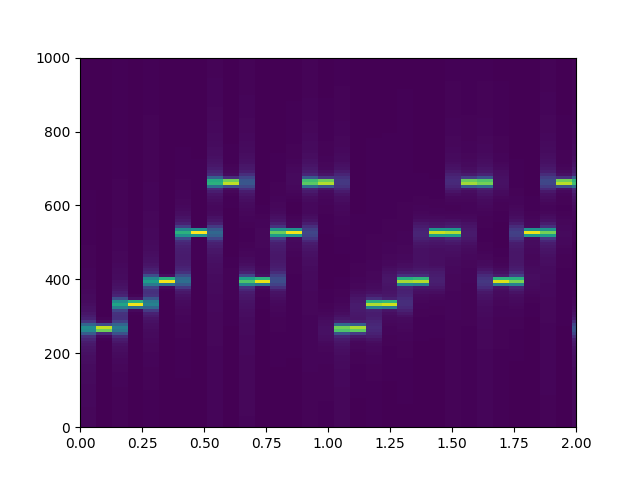
nperseg=1024
周波数分解能はnperseg=256よりも改善していますが、時間分解能が0.064秒で音符の長さ0.125秒の約半分とnperseg=256の場合に較べて相対的にかなり長いため、音程の変化するタイミングがあいまいになっています。
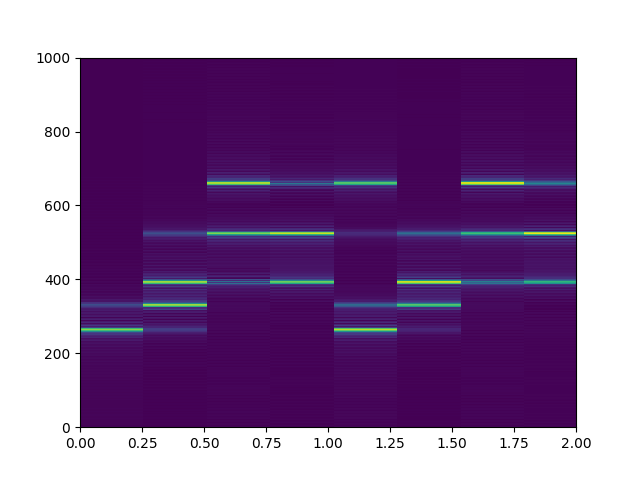
nperseg=4096
時間分解能が0.256秒で音符の長さ0.125秒の倍以上もあるため、もはや音がいつ変化したのか読み取れません。
また窓の大きさを変える
時間分解能も周波数分解能と同じく、サンプリング周波数と窓の大きさによって決まります。サンプリング周波数を \(f_s\) 、窓の大きさを \(n\) とすると、
時間の目盛りの刻み幅は \(\displaystyle\frac{1}{2}\times\frac{n}{f_s}\)
となります。
ここまでの話で判るように、時間分解能(時間の目盛りの刻み幅)を\(\Delta t\)、周波数分解能(周波数の目盛りの刻み幅)を\(\Delta f\) とすると、常に \(\Delta t\times\Delta f=\displaystyle\frac{1}{2}\) となります。つまり、時間分解能と周波数分解能はトレードオフの関係にあり、どちらか一方の精度を上げると、もう一方の精度は反比例して下がります。また、サンプリング周波数が常識に含まれていないことから、サンプリング周波数を上げても(分析できる周波数の上限は上がりますが)、時間分解能と周波数分解能の両方の精度を同時に上げることには繋がらないことが判ります。
ここまでのまとめ
STFTは、時間分解能と周波数分解能を同時によくすることができないという問題はありますが、周波数成分の時間変化を手軽に知ることができる便利なツールです。
ところで…
npersegですが、デフォルト値が256なのにつられてつい \(2^n\) の値を指定してきましたが、実は任意の整数を指定できますので念のため。
次は逆変換を試してみます。

.png)
.png)
窓256拡大.png)
窓256拡大・理想型-1.png)
窓1024拡大.png)
窓4096拡大.png)

コメント