Pythonの特徴の1つには、科学技術計算のライブラリが充実していることがあるのだそうです。今回はその中でも有名な、NumPy と SciPy を使って観ようと思います。
NumPy は、行列やベクトルの計算を行うためのライブラリです。行列の計算は、図形の回転や拡大・縮小、最小二乗法などのデータ分析、いま流行の機械学習にも利用されているので、行列の計算を簡単に行うことができるようになればプログラムにも幅広い応用ができるようになります。
準備
インストール
NumPy は標準のライブラリではないので、利用するにはインストールする必要があります。
py -m pip install numpy でさっさとインストールしましょう。
C:\> py -m pip install numpy
Collecting numpy
Downloading numpy-1.21.2-cp39-cp39-win_amd64.whl (14.0 MB)
|████████████████████████████████| 14.0 MB 3.3 MB/s
Installing collected packages: numpy
Successfully installed numpy-1.21.2
WARNING: You are using pip version 21.1.3; however, version 21.2.4 is available.
You should consider upgrading via the 'D:\Programs\Python\python.exe -m pip install --upgrade pip' command.
C:\>SciPy も同様、利用するにはインストールする必要があります。
py -m pip install scipy でインストールしましょう。
C:\> py -m pip install scipy
Collecting scipy
Downloading scipy-1.7.1-cp39-cp39-win_amd64.whl (33.8 MB)
|████████████████████████████████| 33.8 MB 6.4 MB/s
Requirement already satisfied: numpy<1.23.0,>=1.16.5 in d:\programs\python\lib\site-packages (from scipy) (1.21.2)
Installing collected packages: scipy
Successfully installed scipy-1.7.1
C:\>Pythonをインタラクティブモードで使用
Pythonには『プログラムを作って動かす』という使い方の他に、その場でコマンドを打ち込み、その度に結果をえながら対話的に操作する『インタラクティブモード』があります。
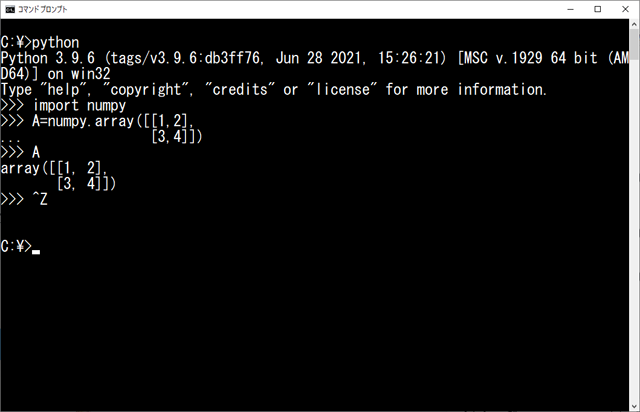
基本的な使い方は以下の通りです。
- インタラクティブモードは、python.exe をコマンドとして実行することで起動できます。
- プロンプトは『>>>』です。
- 制御構文や括弧が閉じていないなど、命令文として完結していないまま改行すると、2行目以降のプロンプトは『…』に変わります。
- 入力した命令文はただちに実行され、それが結果を返すものだった場合にはその場で表示されます。
- インタラクティブモードを終了する場合は、[ctrl]+[Z] を入力し、続いて[Enter]を入力します(Windows系OSの場合)。
今回はまず、このインタラクティブモードを使っていろいろ試してみることにしましょう。
NumPyを試す
ライブラリをimportする
NumPyを使用するには、まずライブラリをimportする必要があります。一度インポートすると、インタラクティブモードを終了するまではNumPyに含まれるメソッドなどが使用できます。
※『>>>』はプロンプトです
>>> import numpy
>>>配列を生成する
NumPy では、行列やベクトルなどを表すのに numpy.ndarray という型を使用します。
※これ以降、この記事では numpy.ndarray を単に配列と記述します。他言語の配列に相当する型は、Pythonではリスト・タプル・dictと称しているので、ご注意下さい。
配列を作成するには、numpy.array() を使用します。書式は以下の通りです。
numpy.array(リストなど)
行列
早速やってみましょう。
>>> A = numpy.matrix([[1,2],[3,4]])
>>>配列は任意の次元のリストによって表されます。
2次元のリストだと行列を表すことができ、この例は
\(A=\left(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right)\)
を表しています。
numpy.array() の返却値は numpy.ndarray型のオブジェクトです。
コマンドプロンプトに続いて配列を代入した変数Aを入力すると、内容の配列が表示されます。
>>> A
array([[1, 2],
[3, 4]])
>>>このように、自動的に縦に揃うように表示してくれます。
ベクトル
1次元のリストを使えば、ベクトルを作成できます。
>>> v = numpy.array([5,6])
>>>これは、
\(\vec{v}=(5,\ 6)\)
を表しています。
コマンドプロンプトに続いて変数vを入力すると、ベクトルの内容が表示されます。
>>> v
array([5, 6])
>>>要素の型
配列の要素のは数値型のいずれかです。一口に数値型といっても整数型と浮動小数点型、さらに整数型だけでも8bit, 16bit, 32bit, int64 のデータ幅の違いと符号付き・符号なしなどのバリエーションがあります。型を指定する場合は、numpy.array() の第2引数で指定します。省略するとリストの要素から自動判別されます。たとえば明示的に32ビット符号付き整数を指定する場合は、
>>> A = numpy.array([[1,2],[3,4]], numpy.int32)
>>>とします。
numpy.matrixによる行列の表現
任意の次元ではなく、2次元の配列=行列を表現するのに特化した型として、numpy.matrix があります。使い方は numpy.array とほぼ同じですが、2次元の配列(行列)しか作れません。
>>> A = numpy.matrix([[1,2],[3,4]])
>>> また生成されたオブジェクトは numpy.matrix型になります。
>>> A
matrix([[1, 2],
[3, 4]])
>>>numpy.matrix() でベクトルを作ろうとすると、1行2列の行列になります。
以下の例では、表示すると [5,6] ではなく[[5,6]] となっています。
>>> v = numpy.matrix([5,6])
>>> v
matrix([[5, 6]])
>>>ほかにも、numpy.array と numpy.matrix では結果が異なる演算があります。
特殊な配列を生成する
単位行列の生成
単位行列とは、\(\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\end{matrix}\right)\) のように左上から右下に向かう対角線上の要素が1で、他が0の正方行列です。後述のドット積で、掛けた相手の行列と同じ結果が出るという特徴があります。
単位行列を生成するには、numpy.identity() メソッドを使用します。引数は大きさです。
>>> E = numpy.identity(3)
>>> E
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
>>>ゼロ行列の生成
ゼロ行列とは、すべての要素が0である行列を言います。
ゼロ行列を生成するには、numpy.zeros() メソッドを使用します。引数にはリスト [行数, 列数] を指定します。
>>> Z = numpy.zeros([2,3])
>>> Z
array([[0., 0., 0.],
[0., 0., 0.]])
>>>配列の計算をする
行列やベクトルの計算をしてみましょう。同じ計算に関数と演算子の両方が定義されているものが多いです。
これ以降の計算例では、
\( A=\left(\begin{matrix} 1 & 2 \\ 3 & 4\end{matrix}\right) ,\hspace{1cm}
B=\left(\begin{matrix} 5 & 6 \\ 7 & 8\end{matrix}\right),\hspace{1cm}
C=\left(\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}\right) \)
\( \vec{v}=(1,\ 2),\hspace{1cm}\vec{w}=(3,\ 4)\)
としています。
同じ条件で試してみたい方は、以下をお使い下さい。一度に全ての行コピペしても動きます。
※Pythonは通常文末の ; は不要ですが、一度に複数の文を実行する場合は ; で区切ります
A = numpy.array([[1,2],[3,4]]);
B = numpy.array([[5,6],[7,8]]);
C = numpy.array([[1,2,3],[4,5,6]]);
v = numpy.array([1,2]);
w = numpy.array([3,4]);
>>> A
array([[1, 2],
[3, 4]])
>>> B
array([[5, 6],
[7, 8]])
>>> C
array([[1, 2, 3],
[4, 5, 6]])
>>> v
array([1, 2])
>>> w
array([3, 4])
>>>加算
同じサイズの配列で同じ位置の要素同士を加算します。
数式で表すと、
\( \left(\begin{matrix} a & b \\ c & d \end{matrix}\right)+
\left(\begin{matrix} e & f \\ g & h \end{matrix}\right)=
\left(\begin{matrix} a+e & b+f \\ c+g & d+h \end{matrix}\right) \)
\( (a,\ b)+(c,\ d)=(a+c,\ b+d) \)
となります。
この計算を行うには、numpy.add()関数、または+演算子を使用します。
実行例
早速やってみましょう。
・行列の場合
>>> numpy.add(A, B)
matrix([[ 6, 8],
[10, 12]])
>>> A + B
matrix([[ 6, 8],
[10, 12]])
>>>\( A+B=\left(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right)+
\left(\begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix}\right)=
\left(\begin{matrix} 1+5 & 2+6 \\ 3+7 & 4+8 \end{matrix}\right)=
\left(\begin{matrix} 6 & 8 \\ 10 & 12 \end{matrix}\right) \)
・ベクトルの場合
>>> numpy.add(v, w)
array([4, 6])
>>> v+w
array([4, 6])
>>>\(\vec{v}+\vec{w}=(1,\ 2)+(3,\ 4)=(1+3,\ 2+4)=(4,\ 6)\)
・計算不可能な場合
加算は同じ大きさの配列同士でなければできないので、A(2行2列)とC(2行3列)で計算しようとするとエラーになります。
>>> A + C
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (2,2) (2,3)
>>> 減算
配列の減算は、同じサイズの配列で同じ位置の要素を減算します。
数式で表すと、
\( \left(\begin{matrix} a & b \\ c & d \end{matrix}\right)+
\left(\begin{matrix} e & f \\ g & h \end{matrix}\right)=
\left(\begin{matrix} a-e & b-f \\ c-g & d-h \end{matrix}\right) \)
\( (a,\ b)-(c,\ d)=(a-c,\ b-d) \)
この計算を行うには、numpy.subtract()関数、または-演算子を使用します。
実行例
早速やってみましょう。
・行列の場合
>>> numpy.subtract(A, B)
matrix([[-4, -4],
[-4, -4]])
>>> A-B
matrix([[-4, -4],
[-4, -4]])
>>>\( A-B=
\left(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right)-
\left(\begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix}\right)=
\left(\begin{matrix} 1-5 & 2-6 \\ 3-7 & 4-8 \end{matrix}\right)=
\left(\begin{matrix} -4 & -4 \\ -4 & -4 \end{matrix}\right) \)
・ベクトルの場合
>>> numpy.subtract(v, w)
array([-2, -2])
>>> v-w
array([-2, -2])
>>>\(\vec{v}-\vec{w}=(1,\ 2)-(3,\ 4)=(1-3,\ 2-4)=(-2,\ -2)\)
・計算不可能な場合
減算は同じ大きさの配列同士でなければ出来ないので、 A(2行2列)とC(2行3列)で計算しようとするとエラーになります。
>>> A - C
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (2,2) (2,3)
>>>スカラー値と配列の積
配列の乗算にはいくつかの種類があります。
まず、スカラー値(単体の数値)と配列の乗算。数式で書くと、
\(k \left(\begin{matrix} a & b \\ c & d \end{matrix}\right) =
\left(\begin{matrix} ka & kb \\ kc & kd \end{matrix}\right) \)
\(k (a,\ b)=(ka,\ kb)\)
です。これは、numpy.multiply()関数、または*演算子を使用します。
実行例
・行列の場合
>>> numpy.multiply(2,A)
array([[2, 4],
[6, 8]])
>>> 2*A
array([[2, 4],
[6, 8]])
>>>\(2A=
2 \left(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right) =
\left(\begin{matrix} 2\times 1& 2\times 2\\ 2\times 3&2\times 4\end{matrix}\right)=
\left(\begin{matrix} 2 & 4 \\ 6 & 8 \end{matrix}\right) \)
・ベクトルの場合
>>> numpy.multiply(3,v)
array([3, 6])
>>> 3*v
array([3, 6])
>>>\(k (a,\ b)=(ka,\ kb)\)
配列の要素同士の乗算
加算や減算と同様、同じ大きさの配列同士で同じ位置の要素を乗算する、という計算もあります。
数学の式ではありませんが、こんな感じです。
\( \left(\begin{matrix} a & b \\ c & d \end{matrix}\right)*
\left(\begin{matrix} e & f \\ g & h \end{matrix}\right)=
\left(\begin{matrix} a\times e & b\times f \\ c\times g & d\times h \end{matrix}\right) \)
\( (a,\ b)*(c,\ d)=(a\times c,\ b\times d) \)
これもスカラー値との乗算と同じく、numpy.multiply()関数、または*演算子を使用します。
※numpy.matrix型の場合、*演算子はドット積を求めるようです
実行例
・行列の場合
>>> numpy.multiply(A,B)
array([[ 5, 12],
[21, 32]])
>>> A*B
array([[ 5, 12],
[21, 32]])
\( A*B=
\left(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right)*
\left(\begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix}\right)=
\left(\begin{matrix} 1\times 5 & 2\times 6 \\ 3\times 7 & 4\times 8 \end{matrix}\right)=
\left(\begin{matrix} 5 & 12 \\ 21 & 32 \end{matrix}\right) \)
・ベクトルの場合
>>> numpy.multiply(v,w)
array([3, 8])
>>> v*w
array([3, 8])
>>>\(\vec{v}*\vec{w}=(1,\ 2)*(3,\ 4)=(1\times 3,\ 2\times 4)=(3,\ 8)\)
ドット積
高校数学で習う、行列の積やベクトルの内積です。
\( \left(\begin{matrix} a & b \\ c & d \end{matrix}\right)
\left(\begin{matrix} e & f \\ g & h \end{matrix}\right)=
\left(\begin{matrix} ae+bg & af+bh \\ ce+dg & cf+dh \end{matrix}\right) \)
\( (a,\ b)\cdot(c,\ d)=ac+bd \)
この計算には、numpy.dot()関数または@演算子(ver.3.5以降)を使用します。
実行例
・正方行列同士の場合
>>> numpy.dot(A,B)
array([[19, 22],
[43, 50]])
>>> A@B
array([[19, 22],
[43, 50]])
>>> \( AB=
\left(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right)
\left(\begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix}\right)=
\left(\begin{matrix} 1\!\times\!5+2\!\times\!7 & 1\!\times\!6+2\!\times\!8\\
3\!\times\!5+4\!\times\!7& 3\!\times\!6+4\!\times\!8 \end{matrix}\right)=
\left(\begin{matrix} 19 & 22 \\ 43 & 50 \end{matrix}\right) \)
・大きさの違う行列の場合
行列の積は、左の行列の列数と右の行列の行数が合っていれば、行列全体の大きさが異なっていても計算できます。よって、A(2行2列)とC(2行3列)でも計算できます。
>>> A @ C
array([[ 9, 12, 15],
[19, 26, 33]])
>>> \( \begin{align}
AC&=
\left(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right)
\left(\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}\right)\\
&=\left(\begin{matrix}
1\!\times\!1+2\!\times\!4 & 1\!\times\!2+2\!\times\!5 & 1\!\times\!3+2\!\times\!6 \\
3\!\times\!1+4\!\times\!4 & 3\!\times\!2+4\!\times\!5 & 3\!\times\!3+4\!\times\!6 \\
\end{matrix}\right)\\
&= \left(\begin{matrix} 9 & 12 & 15 \\ 19 & 26 & 33 \end{matrix}\right)
\end{align}\)
・計算不可能な場合
AとCの順番を逆にすると、2行3列と2行2列の積になってしまい、計算できません。
>>> C @ A
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 2 is different from 3)
>>>・ベクトルの場合
ベクトルの場合は、結果が配列ではなく数値になります。
>>> numpy.dot(v,w)
11
>>> v@w
11
>>>\(\vec{v}\cdot\vec{w}=(1,\ 2)\cdot(3,\ 4)=1\!\times\!3+2\!\times\!4=11\)
・行列とベクトルの場合
座標変換で使用頻度の高い行列とベクトルの乗算も、numpy.dot()関数または@演算子で行います。
>>> numpy.dot(A,v)
array([ 5, 11])
>>> A@v
array([ 5, 11])
>>>\( A\ \vec{v}
=\left(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right)
\left(\begin{matrix} 1 \\ 2 \end{matrix}\right)\
=\left(\begin{matrix}
1\!\times\!1+2\!\times\!2 \\
3\!\times\!1+4\!\times\!2 \\
\end{matrix}\right)\
= \left(\begin{matrix} 5 \\ 11 \end{matrix}\right)
\)
>>> numpy.dot(v,A)
array([ 7, 10])
>>> v@A
array([ 7, 10])
>>>\( \vec{v}\ A
=(1,\ 2) \left(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right)
=(1\!\times\!1+2\!\times\!3,\ 1\!\times\!2+2\!\times\!4
=(7,\ 10)\)
文脈によってベクトルの縦横を読み替えているようです。
※numpy.matrix型の場合は縦ベクトル(2行1列)と横ベクトル(1行2列)は区別されます
クロス積
クロス積とは、ベクトルでいう外積です。
\(\vec{x}=\left(\begin{matrix}a_1\\a_2\\a_3\end{matrix}\right),\hspace{1cm}
\vec{y}=\left(\begin{matrix}b_1\\b_2\\b_3\end{matrix}\right)\)
として、
\(\vec{x}\times\vec{y}
=\left(\begin{matrix}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_1b_2-a_2b_1\end{matrix}\right)\)
クロス積には、numpy.cross()メソッドを使用します。
>>> x = numpy.array([1,2,3])
>>> y = numpy.array([4,5,6])
>>> numpy.cross(x,y)
array([-3, 6, -3])
>>>行列式を求める
行列式の正確な定義は難しいのですが、2次正方行列の場合は、
\(A=\left(\begin{matrix}a&b\\c&d\end{matrix}\right)\) に対して、
\(\mathrm{det} A=ad-bc\)
で表されます。
これを求めるには、numpy.linalg.det() メソッドを使用します。
>>> numpy.linalg.det(A)
-2.0000000000000004
>>>\(\mathrm{det} A = 1\times4-2\times3 = -2\)
のはずなのですが、なぜか 0.0000000000000004 の誤差がでてしまっています。要素は全て整数(int32)で、乗算と加算しか使っていないので浮動小数点数に変換される必然性がなく奇妙なのですが、numpyはこういう仕様のようです。
※sympyという別のモジュールを使うと整数値で計算できるようなので、いずれそちらも試してみます
逆行列を求める
2次正方行列の場合は、
\(A=\left(\begin{matrix}a&b\\c&d\end{matrix}\right)\) に対して、
\(A^{-1}=\displaystyle\frac{1}{ad-bc}\left(\begin{matrix}d&-b\\-c&a\end{matrix}\right)\) で表されます。
逆行列を求めるには、numpy.linalg.inv() メソッドを使用します。
>>> numpy.linalg.inv(A)
array([[-2. , 1. ],
[ 1.5, -0.5]])
>>>\(A^{-1}
=\left(\begin{matrix}1&2\\3&4\end{matrix}\right)^{-1}
=\displaystyle\frac{1}{1\!\times\!4-2\!\times\!3}
\left(\begin{matrix}4&-2\\-3&1\end{matrix}\right)
=\left(\begin{matrix}-2&1\\1.5&-0.5\end{matrix}\right)\)
元の行列と逆行列を掛けると単位行列になるはずなのですが、
>>> D = numpy.linalg.inv(A)
>>> A @ D
array([[1.0000000e+00, 0.0000000e+00],
[8.8817842e-16, 1.0000000e+00]])
>>>逆行列が『ぴったり』な値になったので上手く行くかと思ったのですが、なぜか左下の要素が0になりません…。
numpyを使用した簡単なプログラム
ごく簡単なサンプルを作ってみました。
回転・拡大縮小
図形の回転変換を表す行列
\(\left(\begin{matrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix}\right)\)
および拡大・縮小を表す行列
\(\left(\begin{matrix} s_x & 0 \\ 0 & s_y \end{matrix}\right)\)
を使って点の位置を次々に変化させ、その結果をプロットするプログラムです。
ソースコード
import numpy
import math
from matplotlib import pyplot
#回転行列
rad = math.pi/6
rotationMatrix = numpy.array([[ math.cos(rad), -math.sin(rad)],
[ math.sin(rad), math.cos(rad)]])
#拡大行列
rate = 1.1
expantionMatrix = numpy.array([[ rate, 0],
[ 0, rate]])
dataList = [numpy.array([1,0])]
for i in range(60):
dataList.append(expantionMatrix @ rotationMatrix @ dataList[i])
dataX = []
dataY = []
for vec in dataList:
dataX.append(vec[0])
dataY.append(vec[1])
pyplot.plot(dataX, dataY)
pyplot.show()実行例
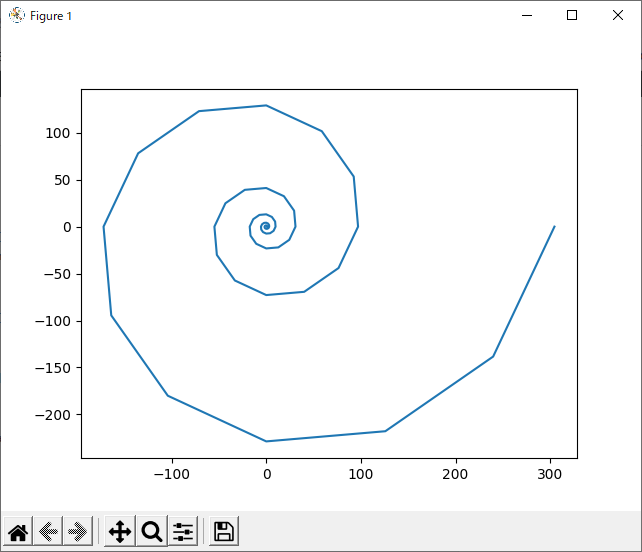
連立方程式解法
二元一次連立方程式
\( \left\{\begin{matrix}ax+by=m\\cx+dy=n\end{matrix}\right. \)
を解くプログラムです。
原理は非常に簡単で、連立方程式を行列を用いて
\(\left(\begin{matrix}a&b\\c&d\end{matrix}\right)
\left(\begin{matrix}x\\y\end{matrix}\right)
=\left(\begin{matrix}m\\n\end{matrix}\right) \)
と表し、
\( \left(\begin{matrix}x\\y\end{matrix}\right)
= \left(\begin{matrix}a&b\\c&d\end{matrix}\right)^{-1}
\left(\begin{matrix}m\\n\end{matrix}\right) \)
としているだけです。
ソースコード
import numpy
print("連立方程式")
print("ax+by=m")
print("cx+dy=n")
print("を解きます。")
print("a,b,c,d,e,fを順に入力して下さい。")
a=float(input("a="))
b=float(input("b="))
c=float(input("c="))
d=float(input("d="))
m=float(input("m="))
n=float(input("n="))
A=numpy.array([[a,b],[c,d]])
v=numpy.array([m,n])
r=numpy.linalg.inv(A)@v
print("x=%(x)f, y=%(y)f" % {"x":r[0], "y":r[1]})実行例
連立方程式
ax+by=m
cx+dy=n
を解きます。
a,b,c,d,e,fを順に入力して下さい。
a=1
b=4
c=1
d=5
e=11
f=13
x=3.000000, y=2.000000とりあえずここまで
今回はリファレンスマニュアルみたいになってしまいました。反省。
次回、もうすこしnumpyをいじってみます。


コメント