numpyには便利な関数があります。
配列対応の数学関数
numpyでは、\(\sin x\)、\(\cos x\) などの三角関数や、\(\log x\)、\(e^x\)などの指数・対数関数など、便利な数学関数がいろいろあります。
いやそんなもの mathモジュールにもあるだろ、と思ってしまうのですが、numpyのものには大きな特徴があります。それは…
引数に配列を渡すと、結果も配列で返してくれる
というものです。
早速試してみましょう。
import numpy
from matplotlib import pyplot
ang = numpy.arange(0.0, 2*numpy.pi, 0.1)
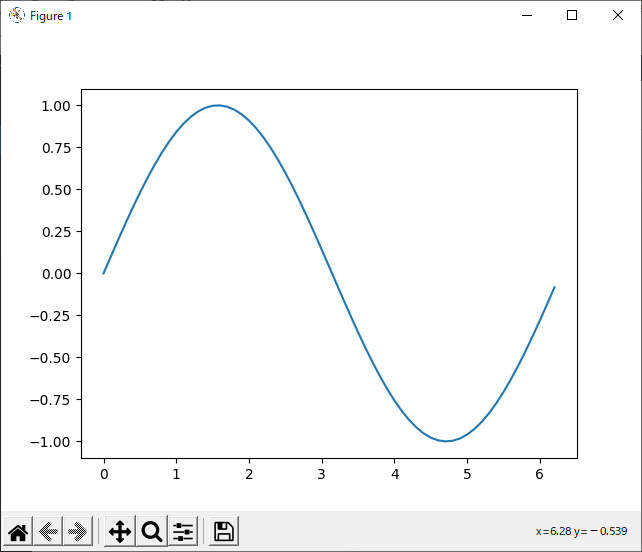
res = numpy.sin(ang)
pyplot.plot(ang,res)
pyplot.show()numpyの他、結果をグラフ表示するためにmatplotlib.pyplotをインポートしています。
今回のポイントはこの2行
ang = numpy.arange(0.0, 2*numpy.pi, 0.1)
res = numpy.sin(ang)numpy.arange()は、自動的に等間隔の数列になった配列を生成します。
numpy.arange(start, stop, step)
最初の値をstartとし、順にstepずつ加算したものを配列に加えつつstop未満の間繰り返し、結果を配列にして返します。start、stop、stepはそれぞれ int、float が使用できます。
インタラクティブモードで試してみましょう。
>>> arg = numpy.arange(0.0, 2*numpy.pi, 0.1)
>>> arg
array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. , 1.1, 1.2,
1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. , 2.1, 2.2, 2.3, 2.4, 2.5,
2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8,
3.9, 4. , 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5. , 5.1,
5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 5.9, 6. , 6.1, 6.2])
>>>numpy.pi は math.pi とおなじく円周率(\(\pi=3.141592\cdots\))です。この例では、
\( 0\leq arg <2\pi \)
の範囲の角度(1周にちょっと足りないですが)を0.1刻みにした配列を作っています。
res = numpy.sin(ang)そして、この numpy.sin() は、引数に配列argを渡すと、結果も配列で返してくれるのです。
試してみましょう。
>>> arg = numpy.arange(0.0, 2*numpy.pi, 0.1) # 再掲
>>> res = numpy.sin(arg)
>>> res
array([ 0. , 0.09983342, 0.19866933, 0.29552021, 0.38941834,
0.47942554, 0.56464247, 0.64421769, 0.71735609, 0.78332691,
0.84147098, 0.89120736, 0.93203909, 0.96355819, 0.98544973,
0.99749499, 0.9995736 , 0.99166481, 0.97384763, 0.94630009,
0.90929743, 0.86320937, 0.8084964 , 0.74570521, 0.67546318,
0.59847214, 0.51550137, 0.42737988, 0.33498815, 0.23924933,
0.14112001, 0.04158066, -0.05837414, -0.15774569, -0.2555411 ,
-0.35078323, -0.44252044, -0.52983614, -0.61185789, -0.68776616,
-0.7568025 , -0.81827711, -0.87157577, -0.91616594, -0.95160207,
-0.97753012, -0.993691 , -0.99992326, -0.99616461, -0.98245261,
-0.95892427, -0.92581468, -0.88345466, -0.83226744, -0.77276449,
-0.70554033, -0.63126664, -0.55068554, -0.46460218, -0.37387666,
-0.2794155 , -0.1821625 , -0.0830894 ])
>>>サンプルプログラムでは、matplotlibで結果をプロットしています。
他言語の感覚だと不思議な感じがしますが、
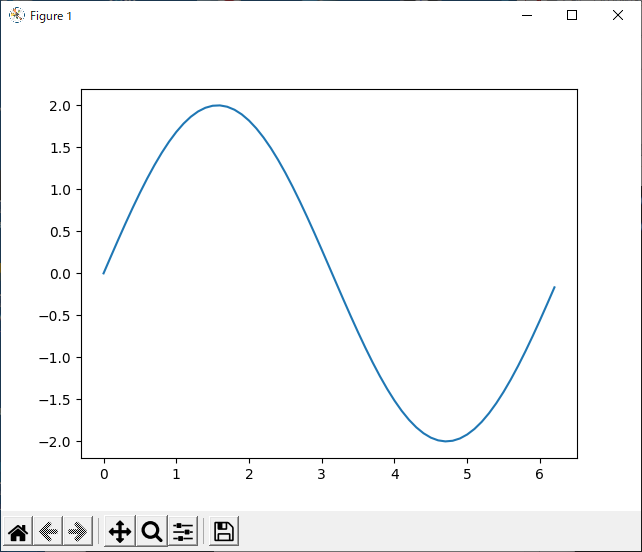
res = 2 * numpy.sin(ang)とすると、ちゃんとすべての要素が2倍になります。
import numpy
from matplotlib import pyplot
ang = numpy.arange(0.0, 2*numpy.pi, 0.1)
res = 2 * numpy.sin(ang)
pyplot.plot(ang,res)
pyplot.show()ちゃんとsinの振幅が2倍になっています。
この機能を利用すると、他言語では繰り返しを使用しなければならない処理を少ない行で記述することができます。
wavファイルを作る
突然気が向いたので、numpyを利用してwav型式(非圧縮PCM)の音声ファイルを作ってみます。
非圧縮PCMのwavファイルは、基本的にはヘッダの後にサンプリングされた値がそのまま並んでいるだけなので、簡単に生成することができます。ついでにバイナリでファイルを読み書きする練習もします。
wavファイルの構造
ヘッダ
ヘッダの情報は以下の通りです(かなり端折っています)
| インデックス | byte数 | 意味 |
|---|---|---|
| 0~3 | 4 | 文字列”RIFF”(0x52 49 46 46)に固定 |
| 4~7 | 4 | 総ファイルサイズ(byte)- 8 |
| 8~11 | 4 | wavファイルでは文字列”WAVE”(0x57 41 56 45)に固定 |
| 12~15 | 4 | wavファイルでは文字列”fmt “(0x66 6D 74 20)に固定 |
| 16~19 | 4 | fmtチャンクのバイト数。非圧縮PCMなら16 |
| 20~21 | 2 | データのフォーマット。非圧縮PCMの場合は 1 |
| 22~23 | 2 | チャンネル数。モノラルなら 1、ステレオなら 2 |
| 24~27 | 4 | サンプリング周波数Hz。たとえば CD なら44.1kHz=44100 |
| 28~31 | 4 | データ速度(byte/s)。ブロックサイズ(Byte)×サンプリング周波数(Hz) |
| 32~33 | 2 | ブロックサイズ(1サンプルあたりのbyte数)量子化ビット数/8×チャンネル数 |
| 34~35 | 2 | 量子化ビット数(bit)。wavなら8か16 |
| 36~39 | 4 | 文字列”data”(0x64 61 74 61)に固定 |
| 40~43 | 4 | 総ファイルサイズ-126 |
wav型式の場合だけ見ると重複している項目があって無駄が多いような気がしますが、RIFFというマルチメディアデータ汎用の共通フォーマットなのでこのようになっています。
データ本体
非圧縮PCMの場合、サンプリングした値がそのまま並べられます。
1つ1つのサンプリングした値は、
量子化ビット数が8の場合、uint8(符号なし8bit整数、0~255)
量子化ビット数が16の場合、int16(符号付き16bit整数、-32768~32767)
サンプリングした値の並べ方は、
1チャンネル(モノラル)の場合は、量子化された値がそのまま連続して並ぶ
2チャンネル(ステレオ)の場合は、左チャンネル→右チャンネル→左チャンネル→と交互に並ぶ。
となっています。
サンプルソースコード
というわけで、作ってみました。
# 正弦波のwavファイルを生成する
import numpy
from sys import byteorder
from matplotlib import pyplot
datafreq = 440 # 発生する音の周波数Hz
samplingfreq = 44100 # サンプリング周波数
ch = 1 # チャンネル数(モノラル=1、ステレオ=2)
quantizationbits = 16 # 量子化ビット数
blocksize = int(ch*quantizationbits/8) # ブロックサイズ(1サンプルあたりのバイト数)
bytespersec = int(samplingfreq*blocksize) # 1秒あたりのバイト数
headersize = 44 # ヘッダサイズ(wavでは44バイト固定)
arg = numpy.deg2rad(numpy.arange(0,samplingfreq,1)/samplingfreq*datafreq*360)
data = numpy.array(2000*numpy.sin(arg), numpy.int16)
datasize = int(len(data)*blocksize) # 全データバイト数
filesize = datasize+headersize # ファイルサイズ
f=open("test.wav","wb")
f.write("RIFF".encode()) # 0- 3 "RIFF"に固定
f.write((filesize - 8).to_bytes(4,byteorder)) # 4- 7 ファイルサイズ-8
f.write("WAVE".encode()) # 8-11 "WAVE"に固定
f.write("fmt ".encode()) #12-15 "fmt "に固定
f.write(0x10.to_bytes(4,byteorder)) #16-19 フォーマットサイズ、デフォルト0x10
f.write(0x01.to_bytes(2,byteorder)) #20-21 フォーマット形式、0x01は非圧縮PCM
f.write(ch.to_bytes(2,byteorder)) #22-23 チャンネル数 0x01はモノラル
f.write(samplingfreq.to_bytes(4,byteorder)) #24-27 サンプリングレート44.1kHz
f.write(bytespersec.to_bytes(4,byteorder)) #28-31 1秒あたりのデータのバイト数
f.write(blocksize.to_bytes(2,byteorder)) #32-33 ブロック境界(1サンプリングあたりのバイト数)
f.write(quantizationbits.to_bytes(2,byteorder)) #34-35 1サンプルあたりのビット数
f.write("data".encode()) #36-39 "data"に固定
f.write((filesize - 126).to_bytes(4,byteorder)) #40-43 ファイルサイズ-126
data.tofile(f) #44- データ本体
f.close()コード解説
データの準備
arg = numpy.deg2rad(numpy.arange(0,samplingfreq,1)/samplingfreq*datafreq*360)
data = numpy.array(2000*numpy.sin(arg), numpy.int16)このサンプルでは周波数datafreq(=440Hz)、振幅2000、1秒分の正弦波を発生させています。numpy.arangeを使い、たった2行で全てのサンプリング値を求めています。
ヘッダの書き込み
いくつか初めて使うメソッドがありますので解説を。
文字列.encode()
文字列をバイト列に変換します。
たとえば
f.write("WAVE".encode())とすると、ファイルに順に 0x57 0x41 0x56 0x45 が書き込まれます。
数値.to_bytes(bytes, byteorder)
数値をバイト列に変換します。引数は、
bytesは、何バイトのバイト列にするか、
byteorderは、複数バイトのデータの時、上位バイトが先か、下位バイトが先か
です。このプログラムの例では sys.byteorder の値をそのまま渡しています。
たとえば
data = 1
f.write(data.to_bytes(2, "little"))とすると、順に 0x01 0x00 がファイルに書き込まれます。
データ本体の書き込み
data.tofile(f)ndarray.tofile()メソッドは、配列ndarrayの各要素の値をバイト列に変換してファイルに書き込みます。このプログラムの例ではあらかじめndarrayの変数dataの要素の方をint16(16ビット符号付き整数)に指定してあるので、tofile()側ではほぼ何も指定することがありません。
この1行で、データ本体すべてが書き込まれます。ループ処理などは不要です。
※ステレオデータの場合はもう少し面倒になると思いますが…。
ファイルができたら、再生してみて下さい。
周波数440Hzとは、音名で言うと A の音です。オーケストラがチューニングに使う音、または昔のテレビ時報の音です。
バイナリファイルからndarrayへの読み込み
サンプルソースコード
import numpy
from matplotlib import pyplot
f=open("test.wav","rb")
f.seek(44)
rectype = numpy.dtype(numpy.int16)
data = numpy.fromfile(f, dtype=rectype)
pyplot.plot(data)
pyplot.show()こちらはかなり手抜きです。まずヘッダの情報はまったく読まず、f.seek(44)で黙って読み飛ばしています。本当はサンプリング周波数や量子化ビット数を読まなければいけないのですが、面倒なので16ビットモノラルと決め打ちしています。
実際の読み込みは非常に簡単です。他言語だとEOFが出るまでちまちま読んでいくのですが、Pythonでは以下の通りです。
rectype = numpy.dtype(numpy.int16)
data = numpy.fromfile(f, dtype=rectype)1行目は個々のデータがint16であると設定しているだけなので、ファイル読み込みは numpy.fromfile()というメソッドだけでやっています。非常に簡単です。
このサンプルでは読み込んだデータを元に波形をプロットしています。ヘッダを読み飛ばしたので横軸はデータのインデックス(0~データ数-1)です。本当なら時間[s]にでもすべきでしょう。
次はこれを使って、信号解析でもやってみましょうか…。


コメント