FFT
フーリエ変換
フーリエ変換について数学的にちゃんと説明するのは難しいのですが(というかブログ主が判ってません)、思いっきり大雑把にいえば、
周期関数(一定のパターンの繰り返し)を、いくつかの sin 関数や cos 関数をつかって表す
というものです。
たとえば楽器の音。オーケストラがチューニングをするとき、それぞれの楽器は440Hz(またはその半分や2倍)の音を出すのですが、このとき楽器ごとに違うパターンの波形が1秒間に440回(またはその半分や2倍)だけ繰り返されています。この波形を sin関数 や cos関数 で表すことができるのです。
信号のサンプリング
ところで、コンピュータが音声などのデータを扱う場合、ほとんどの場合は連続した関数の形ではなく、ごく短い時間毎に値を取得して並べていく、という形を取ります。
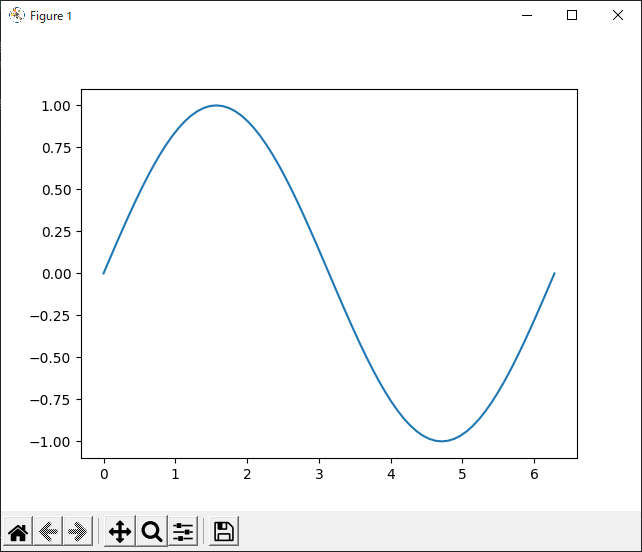
たとえば、先ほどから何度か名前がでているsin関数は、グラフに描くと数のようになります。
これは先に『\(y=\sin x\)』という関数がわかっていてグラフを描いているのですが、コンピュータがこのような波形の信号を受け取って、それをデータ化する場合は、一定間隔でその瞬間ごとの値を測定するようになります。この『瞬間の値を測定』することを『サンプリング』といいます。
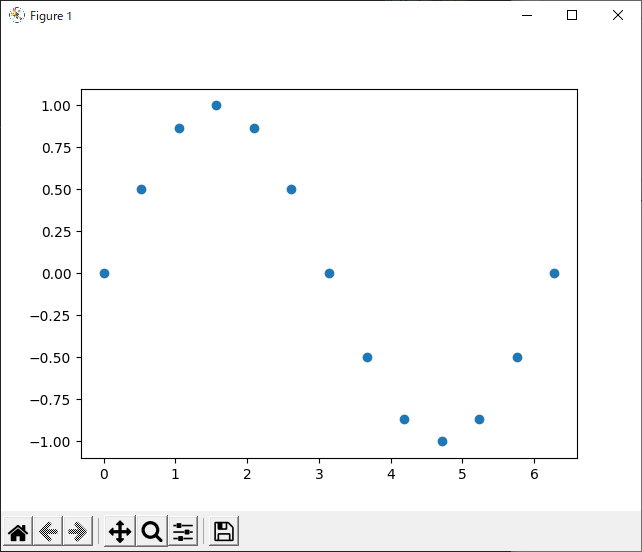
下図は、上で示したsin関数をサンプリングした例です。
この例ではsin関数の1周期(パターン1回分)を13個の点で表しています。このサンプリングの数が多い方が元の波形を細かく表すことができます。1秒間に何回サンプリングを行うか、という数のことを『サンプリング周波数』といいます。
サンプリングでは『その瞬間の値』を測定するのですが、その値は有限桁の数値で表さなければなりません。当然若干の誤差を含みますが、これは数値の桁数が多い方が誤差が小さくなります。この数値の2進数での桁数を『量子化ビット数』といいます。
コンピュータが測定する信号データは、このようにして瞬間瞬間の値を並べたもので、元の関数の形にはなっています。このようなデータを離散値(とびとびのデータ、の意味)といいます。
前回説明したwavファイルのフォーマットが、まさにこの離散値です。
離散フーリエ変換
さて、フーリエ変換をするためには、まず元になる波形を表す関数を用意しなければなりません…といっても、楽器の音の波形の関数なんて判りません。というか判るのならそもそもフーリエ変換をすることにあまり意味がないことになってしまいます。
そこで、離散値を使ってフーリエ変換を行う計算方法が考案されました。これを離散フーリエ変換と言います。これを使うと、コンピュータの測定データを用いて元の信号波形のフーリエ変換を行うことができます。
というわけで、細かい部分を吹っ飛ばしてざっくり言えば、
離散フーリエ変換を使えば、wavファイルのデータを読み込んで、
sin関数やcos関数の組み合わせに変換できる
ということなのです。
FFT
FFTとは、Fast Fourier Transform =高速フーリエ変換の略で、離散フーリエ変換を高速に行うことができるアルゴリズムのことです。具体的なアルゴリズムの説明はここではしませんが、
Python の NumPyモジュールには、FFTのためのメソッドが実装されています。
つまり、
ほんの数行のプログラムで、FFTが行えるのです。
早速実験、の前に、サンプル波形ジェネレータ
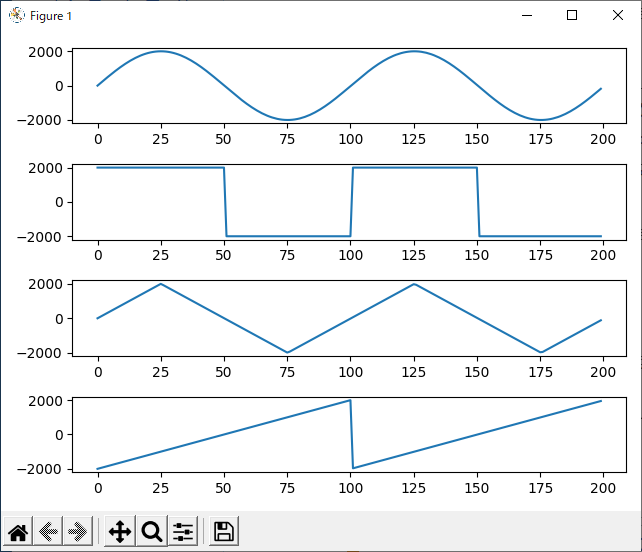
いろいろな波形によって結果がどう変わるかを試すために、前回やっつけで作成した正弦波(sin波)発生プログラムを改良して、以下の4種類の波形を出力できるようにしました。
上から、
正弦波(sin wave)
矩形波(square wave)
三角波(triangle wave)
のこぎり波(sawtooth wave)
といいます。信号波形が話題になるときにはよく例として使われる波形です。
サンプルソースコード
import numpy
from sys import byteorder
from matplotlib import pyplot
datafreq = 440 # 発生する音の周波数Hz
samplingfreq = 44100 # サンプリング周波数
ch = 1 # チャンネル数(モノラル=1、ステレオ=2)
quantizationbits = 16 # 量子化ビット数
blocksize = int(ch*quantizationbits/8) # ブロックサイズ(1サンプルあたりのバイト数)
bytespersec = int(samplingfreq*blocksize) # 1秒あたりのバイト数
headersize = 44 # ヘッダサイズ(wavでは44バイト固定)
def fileout(data, filename):
f = open(filename, "wb")
f.write("RIFF".encode()) # 0- 3 "RIFF"に固定
f.write((filesize - 8).to_bytes(4,byteorder)) # 4- 7 ファイルサイズ-8
f.write("WAVE".encode()) # 8-11 "WAVE"に固定
f.write("fmt ".encode()) #12-15 "fmt "に固定
f.write(0x10.to_bytes(4,byteorder)) #16-19 フォーマットサイズ、デフォルト0x10
f.write(0x01.to_bytes(2,byteorder)) #20-21 フォーマット形式、0x01は非圧縮PCM
f.write(ch.to_bytes(2,byteorder)) #22-23 チャンネル数 0x01はモノラル
f.write(samplingfreq.to_bytes(4,byteorder)) #24-27 サンプリングレート44.1kHz
f.write(bytespersec.to_bytes(4,byteorder)) #28-31 1秒あたりのデータのバイト数
f.write(blocksize.to_bytes(2,byteorder)) #32-33 ブロック境界(1サンプリングあたりのバイト数)
f.write(quantizationbits.to_bytes(2,byteorder)) #34-35 1サンプルあたりのビット数
f.write("data".encode()) #36-39 "data"に固定
f.write((len(data)*2).to_bytes(4,byteorder)) #40-43 dataチャンクのデータバイト数
data.tofile(f) #44- データ本体
f.close()
deg = (numpy.arange(0,samplingfreq,1)/samplingfreq*datafreq*360) % 360
rad = numpy.deg2rad(deg)
sinwave = numpy.array(2000*numpy.sin(rad), numpy.int16)
squarewave = numpy.array(2000*numpy.sign(180-deg), numpy.int16)
trianglewave = numpy.array(2000*numpy.abs((deg+270)%360-180)/90-2000, numpy.int16)
sawtoothwave = numpy.array(2000*(deg/180-1), numpy.int16)
datasize = int(len(deg)*blocksize) # 全データバイト数
filesize = datasize+headersize # ファイルサイズ
fileout(sinwave, "sinwave.wav")
fileout(squarewave, "squarewave.wav")
fileout(trianglewave, "trianglewave.wav")
fileout(sawtoothwave, "sawtoothwave.wav")
fig = pyplot.figure()
plot1 = fig.add_subplot(4,1,1)
plot1.plot(sinwave[0:int(samplingfreq/datafreq*2)])
plot2 = fig.add_subplot(4,1,2)
plot2.plot(squarewave[0:int(samplingfreq/datafreq*2)])
plot3 = fig.add_subplot(4,1,3)
plot3.plot(trianglewave[0:int(samplingfreq/datafreq*2)])
plot4 = fig.add_subplot(4,1,4)
plot4.plot(sawtoothwave[0:int(samplingfreq/datafreq*2)])
fig.tight_layout()
pyplot.show()実行する
プログラムを実行すると、カレントディレクトリに
sinwave.wav
squarewave.wav
trianglewave.wav
sawtoothwave.wav
の4つのファイルを生成します。いずれも量子化440Hz、1秒分、ビット数16、サンプリング周波数44.1kHz、モノラルのリニアPCM型データです。Windows環境ではファイルをダブルクリックすると再生できます。視聴は以下でどうぞ。
耳で聞くと、4つの音の高さは同じなのですが、
sinwave.wav → trianglewave.wav → squarewave.wav → sawtoothwave.wav
の順に『柔らかく落ち着いた音』から『硬く強い音』のように音色が変化してきこえると思います。
FFTプログラム
今回はFFTを利用して、信号に含まれる周波数成分(sinやcosに分解した1つ1つの周波数)を分析します。
サンプルソースコード
import numpy
from scipy import signal
from matplotlib import pyplot
samplingfreq = 44100
quantizationbits = 16
f = open("sinwave.wav", "rb")
f.seek(44) # データセクションの先頭まで移動
data = numpy.fromfile(f, dtype="int16")
N = len(data) # 全サンプリングデータ数
dt = 1/samplingfreq # サンプリング間隔(秒))
# FFT
F = numpy.fft.fft(data) # フーリエ変換(結果は複素数の配列)
freq = numpy.fft.fftfreq(N, d=dt) # 周波数の配列
amp = numpy.abs(F/(N/2)) # 振幅(複素数で表された成分の絶対値)を取得
# ここからピーク検出
idx = signal.argrelmax(amp)[0]
max = amp.max() # 振幅の最大値を取得
peak_cut = max*0.05 # 最大振幅の成分の 5% に満たない成分はノイズとみなしてカット
idx = idx[(amp[idx] > peak_cut) & (idx <= N/2)] # peak cut以下のものは消す
for i in idx:
print(freq[i], amp[i])
fig = pyplot.figure()
plot1 = fig.add_subplot(2,1,1)
plot1.plot(data[0:500])
plot2 = fig.add_subplot(2,1,2)
plot2.plot(freq[1:int(N/2)], amp[1:int(N/2)])
fig.tight_layout()
pyplot.show()
コード解説
ヘッダ部
import numpy
from scipy import signal
from matplotlib import pyplot
samplingfreq = 44100
quantizationbits = 16numpy、matplotlib.pyplot の他、信号の極大値を検出するために scipy.signalをインポートしています。
このサンプルプログラムでは、上のサンプル波形ジェネレータで生成したファイルを使用する前提のため、samplingfreq(サンプリング周波数)とquantizationbits(量子化ビット数)はそれぞれ44.1kHz、16ビットの固定にしてありますが、汎用性を持たせるならwavファイルのヘッダから読み取るようにすると良いでしょう。
※SciPy は標準のライブラリではないので、利用するにはインストールする必要があります。まだ入れていない場合は、py -m pip install scipy でインストールしましょう。
C:\> py -m pip install scipy
Collecting scipy
Downloading scipy-1.7.1-cp39-cp39-win_amd64.whl (33.8 MB)
|████████████████████████████████| 33.8 MB 6.4 MB/s
Requirement already satisfied: numpy<1.23.0,>=1.16.5 in d:\programs\python\lib\site-packages (from scipy) (1.21.2)
Installing collected packages: scipy
Successfully installed scipy-1.7.1
C:\>波形データの読み込み
f = open("sinwave.wav", "rb")
f.seek(44) # データセクションの先頭まで移動
data = numpy.fromfile(f, dtype="int16")
open() で読み込むファイルを指定しています。サンプルでは”sinwave.wav”となっていますが、この部分を書き換えて4つの波形それぞれで試してみましょう。
ファイルは”rb”(バイナリ読み取り)モードで開いています。
f.seek(44)でヘッダ部を読み飛ばし、波形データ本体の先頭までファイルポインタを進めています。手抜きです。
numpy.fromfile() でデータを一気に読み込んでいます。読み込んだバイナリデータは dtype=によって指定されたフォーマットとしてデコードされ、ndarrayに順に要素として格納され、返されます。
なお、dtype=”int16″は16ビット符号付き整数の意味で、量子化ビット数16のwavファイルの場合はこの指定となります。量子化ビット数8のwaveファイル場合は符号なしなのでdtype=”uint8″を指定します。
このサンプルではモノラル音声なのでサンプリングされたデータが連続して並んでいますが、ステレオの場合にはファイル内に
左チャンネルのデータ → 右チャンネルのデータ → 左チャンネルのデータ → …
という型式でデータが並んでいるため、
偶数番目のデータ(dataの0,2,4,6,…):左チャンネルのデータ
奇数番目のデータ(dataの1,3,5,7,…):右チャンネルのデータ
となります。ステレオのデータをFFTで分析する場合は、偶数番目と奇数番目のデータを別の配列に分離する必要があります。
定数の計算
N = len(data) # 全サンプリングデータ数
dt = 1/samplingfreq # サンプリング間隔(秒))FFTの際に必要になる数をあらかじめ計算しています。Nはデータ総数、dtはサンプリングの間隔時間です。
FFT(フーリエ変換)
F = numpy.fft.fft(data) # 離散フーリエ変換(結果は複素数の配列)
freq = numpy.fft.fftfreq(N,d=dt) # 周波数の配列
amp = numpy.abs(F/(N/2)) # 振幅(複素数で表された成分の絶対値)を取得フーリエ変換の本体はたったこれだけです。
変換によって取得できる式
このプログラムでは、元の波形を
\[\displaystyle F(t)=\sum^{\frac{N}{2}-1}_{k=0}A_k\sin(2\pi f_k t) \]
という形に変換します。話を簡単にするため、複素成分・位相などを省き、単純に複数の周波数成分(\(f_0,\ f_1,\ f_2,\ \cdots\))の sin関数の和として表しています。
上式の\(A_k\)、\(f_k\) と、ソースコードの変数 amp[k]、freq[k] がそれぞれ対応します。
numpy.fft.fft(サンプリングデータ)
によって、サンプリングデータをフーリエ変換します。返却値は複素数の配列です。
振幅を取得する周波数の配列を求める
次の
numpy.fft.fftfreq(データ数, サンプリング間隔)
では、周波数の配列 \(f_0,\ f_1,\ f_2,\ \cdots\) を生成しています。これは実はサンプリングデータの中身ではなく、サンプリングデータ数Nとサンプリング間隔dtだけで決まり、
\[f_k = \displaystyle\frac{k}{N\times dt}\]
で求められます。サンプリング周波数を \(f_s\) とすると、\(dt=\displaystyle\frac{1}{f_s}\) ですから、
\[f_k = \displaystyle\frac{k}{N}f_s\]
となります。ただし、\(0\leq k < \frac{N}{2}\) です。つまり、表現できる周波数成分は\(\frac{1}{2}f_s\)未満となり、サンプリング周波数の\(\frac{1}{2}\)以上の成分はフーリエ変換では分析できません。
…というか、そもそもサンプリングでは、サンプリング周波数の半分を超える成分が表現できません(これを標本化定理、またはシャノン・染谷の定理といいます)
式から判るように、サンプリング周波数が低いほど・標本データ数が多いほど分析可能な周波数の間隔が狭く(より細かく分析可能に)なります。今回のサンプルでは、標本数\(N=44100\)・サンプリング周波数\(f_s=44100 \mathrm{Hz}\) なので、配列 freq の \(0\) ~ \(\frac{N}{2}-1\)の範囲には、
freq = [ 0, 1, 2, … ,22049 ]と、1Hz刻みの周波数が入ります。
ところで、freq の要素数はNなので、周波数の列には配列freqの前半だけしか使っていません。後半には『負の周波数』が入っているのですが、今回は使用しません。
各周波数成分の振幅の取得
amp = numpy.abs(F/(N/2)) numpy.abs は複素数の絶対値を求める関数です。ちょっとややこしいのですが、配列Fの要素を\(\frac{N}{2}\)で割って絶対値を求めると、各周波数成分の振幅になります。
ここまでの処理で、配列freqと配列ampは、
周波数freq[0]の周波数成分の振幅がamp[0]、周波数freq[1]の周波数成分の振幅がamp[1]…
という関係になっています。
ピークの検出
idx = signal.argrelmax(amp)[0] FFTの結果は、1Hz刻みの各周波数成分の振幅という形で得られます。そのうち振幅が極大となっている成分が元の波形に含まれている周波数です。これを検出します。
signal.argrelmax(配列)[0]
signal.argrelmax()関数は、与えられた配列の中で極大となっている(前後の要素より大きい)要素のインデックスの配列のタプルを返します。配列ではなく配列のタプルです。多次元のデータに対応するためにこういう仕様になっているようですが、今回は1次元のデータなので[0]しか使っていません。
max = amp.max() # 振幅の最大値を取得
peak_cut = max*0.01 # 最大振幅の成分の 1% に満たない成分はノイズとみなしてカット
idx = idx[(amp[idx] > peak_cut) & (idx <= N/2)] # peak cut以下のものは消すノイズをカットするため、振幅が最大値の1%に満たないものは省いています。
周波数と振幅の表示
for i in idx:
print(freq[i], amp[i])idx は振幅が極大となった成分のインデックスの配列なので、frec と amp から該当する値を順次とりだして表示しています。
グラフの表示
fig = pyplot.figure()
plot1 = fig.add_subplot(2,1,1)
plot1.plot(data[0:500])
plot2 = fig.add_subplot(2,1,2)
plot2.plot(freq[1:int(N/2)], amp[1:int(N/2)])
fig.tight_layout()
pyplot.show()複数のグラフを表示するのは初めてなので、いくつか新しいメソッドを使用しています。順に見ていきましょう。
fig = pyplot.figure()figは、図全体を表します。このプログラムでは2つのグラフを表示するので、その土台のようなものだと思えばいいでしょう。
plot1 = fig.add_subplot(row, col, no)は、複数のグラフを並べるためのものです。
fig上に、縦にrow個、横にcol個のグラフを並べ、そのうちno番目のグラフを作成する、という意味です。生成されたオブジェクトplot1に対して、グラフの描画を行います。
plot1.plot(data[0:500])data全てを表示すると波形が密になりすぎてまったく読み取れないので、サンプリング値の最初の500個分だけを描画しています。今回のサンプルデータ、周波数440Hzでは約2波長分です。
plot2.plot(freq[1:int(N/2)], amp[1:int(N/2)])周波数を横軸、振幅を縦軸としてグラフを表示します。このように、周波数成分ごとに振幅を表したグラフを周波数スペクトルといいます。freq、ampともに要素はN個ありますが、前半だけしか描画しません。
実際に分析してみよう
正弦波
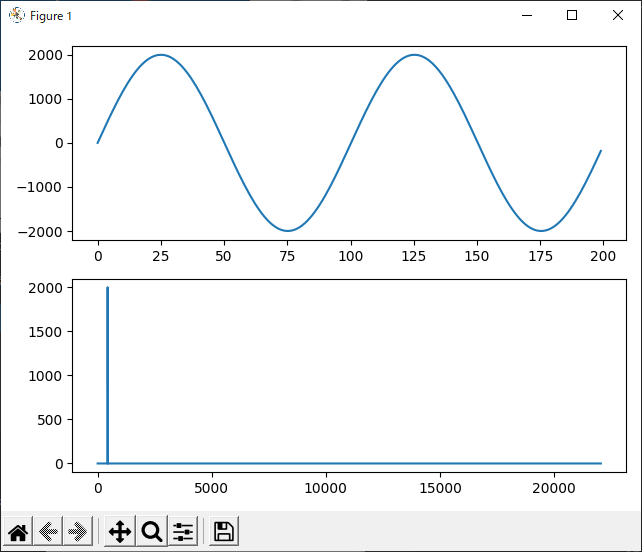
まず、sinwave.wavを入力してみましょう。
下段のスペクトルを見ると、左の方に鋭いピークが1つだけあります。
コンソールには周波数と振幅が表示されています。
440.0 1999.3372311610035
周波数440Hzの成分が、振幅1999.3372…
となっています。元の信号は周波数440Hz、振幅2000の正弦波ですから、ちゃんと分析できていることが判ります。
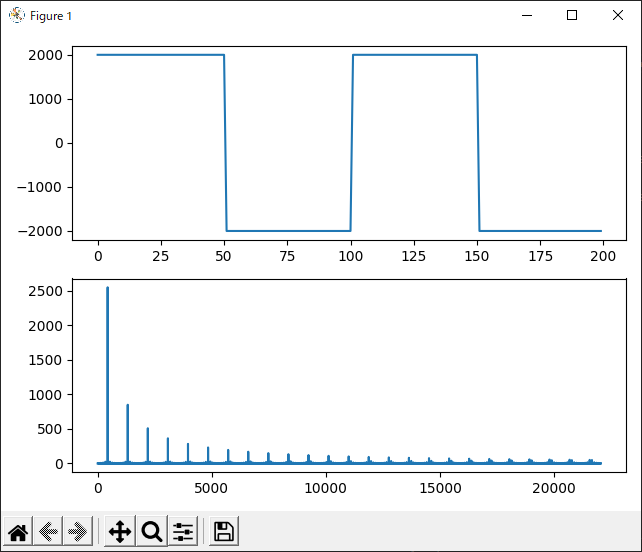
矩形波
open()の中のファイル名を “squarewave.wav” に書き換えて、矩形波を分析してみましょう。
スペクトルを見ると、左に大きなピークがあり、そこから周波数の高い方に向かって等間隔にだんだん小さくなりながら極大点が続いています。
極大点の具体的な周波数と振幅を確認すると、
440.0 2546.4793048533425
1320.0 848.8270093061321
2200.0 509.2968948106803
3080.0 363.784234752593
3960.0 282.9440595085929
4840.0 231.50046827277666
5720.0 195.8858068894044
6600.0 169.7685034194574
7480.0 149.7965491896255
8360.0 134.02930759982902
となっています。よく見ると、いちばん低い周波数440Hzの成分を基準にして、
周波数が3倍で振幅が1/3
周波数が5倍で振幅が1/5
周波数が7倍で振幅が1/7
…
という成分が含まれていることが判ります。
いちばん低い周波数は『波形パターンが1秒間に何回繰り返されているか』を表すもので、基本周波数とよびます。この分析結果からわかるように、正弦波以外の波形には基本周波数の整数倍の周波数成分が多く含まれています。これを『高調波』といい、基本周波数のn倍の成分のことを『第n高調波』といいます。音楽の世界で『倍音』といっているのはこの高調波成分のことです。
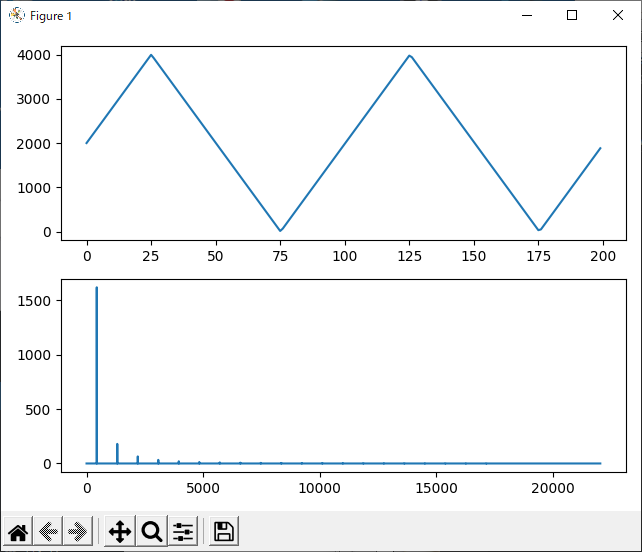
三角波
open()の中のファイル名を “trianglewave.wav” に書き換えて、三角波を分析してみましょう。
スペクトルを見ると、左側に大きなピークがあり、周波数の高い方に向かって等間隔で極大点が並んでいるのは矩形波と同じですが、振幅がかなり違います。
周波数と振幅を確認すると、
440.0 1621.1392092288168
1320.0 180.12666549764924
2200.0 64.84572769130284
3080.0 33.0846593293995
3960.0 20.01390773361352
となっています。周波数440Hzの成分を基準とすると、
周波数が3倍で振幅が1/9
周波数が5倍で振幅が1/25
周波数が7倍で振幅が1/49
周波数が9倍で振幅が1/81
となっています。
のこぎり波
open()の中のファイル名を “sawtoothwave.wav” に書き換えて、のこぎり波を分析してみましょう。
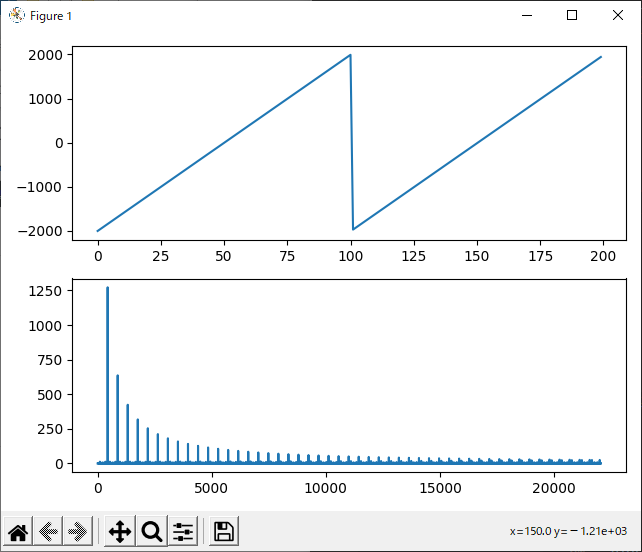
非常に多くの極大点が出ています。しかも矩形波や三角波よりも間隔が狭いようです。
周波数と振幅を確認しましょう。
※ノイズが多くでたのでカットオフを『最大値の1%以下』から『最大値の2%以下』に変更しました
440.0 1272.6037204281054
880.0 636.6213960959553
1320.0 424.2015084283837
1760.0 318.3112466688463
2200.0 254.52309005821854
…
矩形波や三角波では基本周波数の奇数倍の成分しかありませんでしたが、のこぎり波では
周波数が2倍で振幅が1/2
周波数が3倍で振幅が1/3
周波数が4倍で振幅が1/4
周波数が5倍で振幅が1/5
…
となっています。
波形の合成
FFTでの分析結果を基に、sin波を合成して元の波形になるかを確かめてみましょう。
サンプルソースコード
# 正弦波のwavファイルを生成する
import numpy
from sys import byteorder
from matplotlib import pyplot
deg = (numpy.arange(0,720)) % 360
rad = numpy.deg2rad(deg)
#お手本波形
squarewave = numpy.array(2000*numpy.sign(180-deg), numpy.int16)
trianglewave = numpy.array(2000*numpy.abs((deg+270)%360-180)/90-2000, numpy.int16)
sawtoothwave = numpy.array(2000*(deg/180-1), numpy.int16)
#合成波形
squarewave_syn = numpy.array(2500*numpy.sin(rad)+833*numpy.sin(3*rad)+500*numpy.sin(5*rad)+357*numpy.sin(7*rad)+278*numpy.sin(9*rad), numpy.int16)
trianglewave_syn = numpy.array(1620*numpy.sin(rad)+180*numpy.sin(3*rad)+65*numpy.sin(5*rad)+33*numpy.sin(7*rad)+20*numpy.sin(9*rad), numpy.int16)
sawtoothwave_syn = numpy.array(1200*numpy.sin(rad)+600*numpy.sin(2*rad)+400*numpy.sin(3*rad)+300*numpy.sin(4*rad)+240*numpy.sin(5*rad), numpy.int16)
pyplot.plot(squarewave, color="red")
pyplot.plot(squarewave_syn, color="blue")
pyplot.show()それぞれの波形を2周期分描くだけの簡単なプログラムです。
このサンプルでは矩形波をプロットするようになっているので、pyplot.plot()の中を書き換えてそれぞれのグラフを描画します。
矩形波
波形の合成関数は以下のようになります。
squarewave_syn = numpy.array(2500*numpy.sin(rad)+833*numpy.sin(3*rad)+500*numpy.sin(5*rad)+357*numpy.sin(7*rad)+278*numpy.sin(9*rad), numpy.int16)ごちゃごちゃするので、基本周波数(f_0)のかわりに基本の角振動数(\omega_0=2\pi f_0)、基本周波数成分の振幅を(A)として式を書き直すと、
\(\displaystyle A\sin(\omega_0 t)+\frac{1}{3}A\sin(3\omega_0 t)+\frac{1}{5}A\sin(5\omega_0 t) + \frac{1}{7}A\sin(7\omega_0 t) + \frac{1}{9}A\sin(9\omega_0 t) \)
となっています。プログラムでは配列変数radが\(\omega_0 t\)に相当します。
本来はsinが無数に連なるのですが、係数の小さな項は無視して最初の5項のみ合成しています。
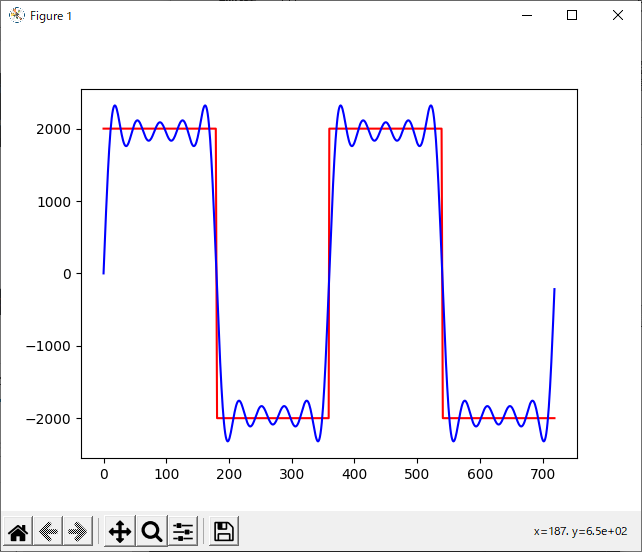
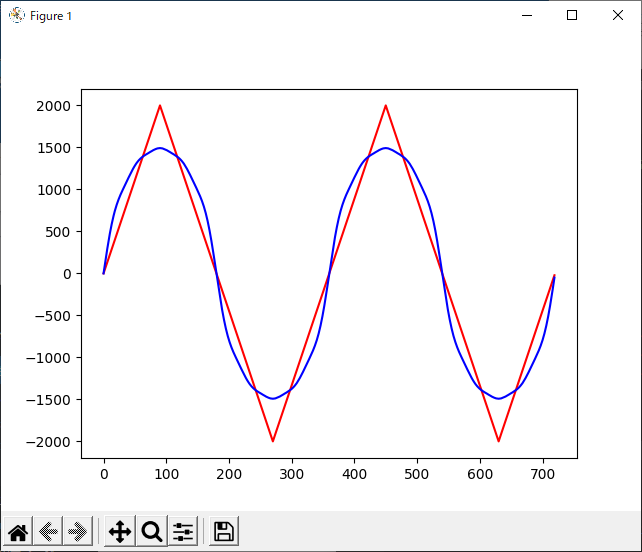
計算結果をプロットしてみると下図のようになります。赤い線がサンプル波形ジェネレータで生成した『お手本』、青い線がsinを合成した波形です。
かなりそれっぽい形になりました。この例では成分を5つしか合成していませんが、もっと高い周波数の成分まで足していけばさらにお手本に近づきそうです。
三角波
ソースコードの一番下の部分を以下のように書き換えて、三角波の合成波形を見てみましょう。
pyplot.plot(trianglewave, color="red")
pyplot.plot(trianglewave_syn, color="blue")
pyplot.show()三角波の合成関数は、
trianglewave_syn = numpy.array(1620*numpy.sin(rad)+180*numpy.sin(3*rad)+65*numpy.sin(5*rad)+33*numpy.sin(7*rad)+20*numpy.sin(9*rad), numpy.int16)\(\displaystyle A\sin(\omega_0 t)+\frac{1}{9}A\sin(3\omega_0 t)+\frac{1}{25}A\sin(5\omega_0 t) + \frac{1}{49}A\sin(7\omega_0 t) + \frac{1}{81}A\sin(9\omega_0 t) \)
となります。これも最初の5項のみの合成です。
波形をプロットすると、
となってしまい、あまりお手本と合っていません。
実はこれは、各周波数成分の位相を考慮していないためです。奇数番目の項の符号を反転して(位相を\(\pi\)だけずらして)、
trianglewave_syn = numpy.array(1620*numpy.sin(rad)-180*numpy.sin(3*rad)+65*numpy.sin(5*rad)-33*numpy.sin(7*rad)+20*numpy.sin(9*rad), numpy.int16)\(\displaystyle A\sin(\omega_0 t)-\frac{1}{9}A\sin(3\omega_0 t)+\frac{1}{25}A\sin(5\omega_0 t) -\frac{1}{49}A\sin(7\omega_0 t) + \frac{1}{81}A\sin(9\omega_0 t) \)
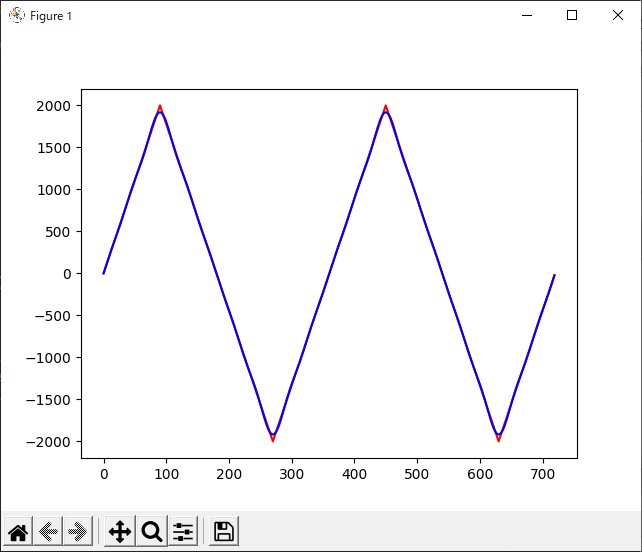
とすると、
このように、非常に良くお手本と合うようになります。
のこぎり波
ソースコードの一番下の部分を以下のように書き換えて、のこぎり波の合成波形を見てみましょう。
pyplot.plot(sawtoothwave, color="red")
pyplot.plot(sawtoothwave_syn, color="blue")
pyplot.show()のこぎり波の合成関数は、
sawtoothwave_syn = numpy.array(1200*numpy.sin(rad)+600*numpy.sin(2*rad)+400*numpy.sin(3*rad)+300*numpy.sin(4*rad)+240*numpy.sin(5*rad), numpy.int16)\(\displaystyle A\sin(\omega_0 t)+\frac{1}{2}A\sin(2\omega_0 t)+\frac{1}{3}A\sin(3\omega_0 t) + \frac{1}{4}A\sin(4\omega_0 t) + \frac{1}{5}A\sin(5\omega_0 t) \)
です。
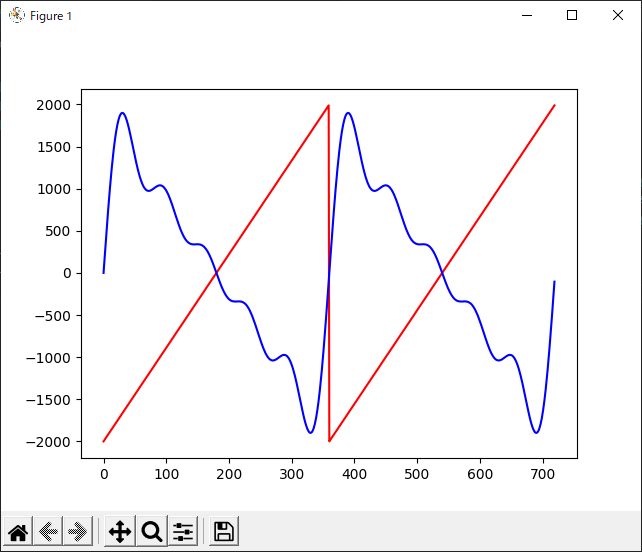
この波形をプロットすると、
となってしまい、お手本とまったく合っていません。しかしよく見ると、上下を逆さま(符号反転、sin関数の場合は位相を\(\pi\)ずらす)にすればよさそうです。
式全体にマイナスをつけてしまいましょう。
sawtoothwave_syn = -numpy.array(1200*numpy.sin(rad)+600*numpy.sin(2*rad)+400*numpy.sin(3*rad)+300*numpy.sin(4*rad)+240*numpy.sin(5*rad), numpy.int16)\(-\left\{A\sin(\omega_0 t)+\frac{1}{2}A\sin(2\omega_0 t)+\frac{1}{3}A\sin(3\omega_0 t) + \frac{1}{4}A\sin(4\omega_0 t) + \frac{1}{5}A\sin(5\omega_0 t) \right\}\)
これをプロットすると、
このように、かなり近い波形になります。
まとめ
というわけで、今回は Python の NumPy モジュールを利用して、FFTの実験をしてみました。NumPyのドキュメントに『fft』の文字を発見して即やっつけで作り始めたのですが、周波数成分を調べる程度のプログラムならすぐに作れるんですね…。
ブログ主が知識0の状態でPythonの教科書を手に取ってからまだ2週間足らずですが、驚くほど簡単にここまで進んでしまいました。Pythonという言語でのプログラムの作りやすさ故でしょう。
さて、もうすぐ期末試験なので、ここまで連続でやってきたPython短期集中勉強会はちょっとお休みです。



コメント