前回で一段落ついたことにして、タイトルから『短期集中』を取りました。今後は何か思いついたときに不定期に書いていきます。
前回の補足(位相の取得)
フーリエ変換によって求める式を、少し修正します。
\[\displaystyle F(t)=\sum^{\frac{N}{2}-1}_{k=0}A_k\sin(2\pi f_k t+\phi_k) \]
\(+\phi_k\) という項を増やしました。実は僕が普段扱っている世界では周波数成分だけが問題で位相はほぼ結果に影響を与えないので無視するクセがついてしまっていたのですが、やはりつけておいたほうがいいかな…と思い直しました。
前回も書いたとおり、numpy.fft.fft() メソッドは複素数列を返します。絶対値が角周波数成分の振幅を表すのは既に説明したとおりですが、実は偏角が位相を表しています。numpyには複素数から偏角を求める numpy.angle() メソッドがあるので、これを使えば簡単に位相を取得することができます。
具体的に前回の分析プログラムを修正するには、
F = numpy.fft.fft(data) # 離散フーリエ変換(結果は複素数の配列)
freq = numpy.fft.fftfreq(N,d=dt) # 周波数の配列
amp = numpy.abs(F/(N/2)) # 振幅(複素数で表された成分の絶対値)を取得この部分に
F = numpy.fft.fft(ldata) # フーリエ変換(結果は複素数の配列)
freq = numpy.fft.fftfreq(N,d=dt) # 周波数の配列
amp = numpy.abs(F/(N/2)) # 振幅(複素数で表された成分の絶対値)を取得
pha = numpy.angle(F) # 位相(複素数で表された成分の偏角)を取得1行追加するだけです。変数 pha に位相の配列が入ります。
表示部分も
for i in idx:
print(freq[i], amp[i], pha[i])として位相を表示できるようにしましょう。
ではこれで、また三角波を分析してみましょう。
結果は、
440.0 1620.5034168469622 -1.570796238271722
1320.0 180.33878698737297 1.5707974994728406
2200.0 64.71840425487723 -1.5707942245424795
3080.0 33.17568903595271 1.5708027013216688
となります。440Hzの成分と2200Hzの成分の位相が-1.570…、1320Hzの成分と3080Hzの成分が1.570…で、前回の波形合成の時に波形が一致するように調節したのと同じく差が 3.141…\(=\pi\) になっていることが判ります。
母音を分析・合成
次に、計算で合成したWavファイルではなく、実際の音を分析してみましょう。
まずは分析
『あ・い・う・え・お』の5音の周波数分析をしてみましょう。
今回サンプルに使用した音声は、高さはA3、前回のサンプルで使った440Hzのオクターブ下で基本周波数は220Hzです。
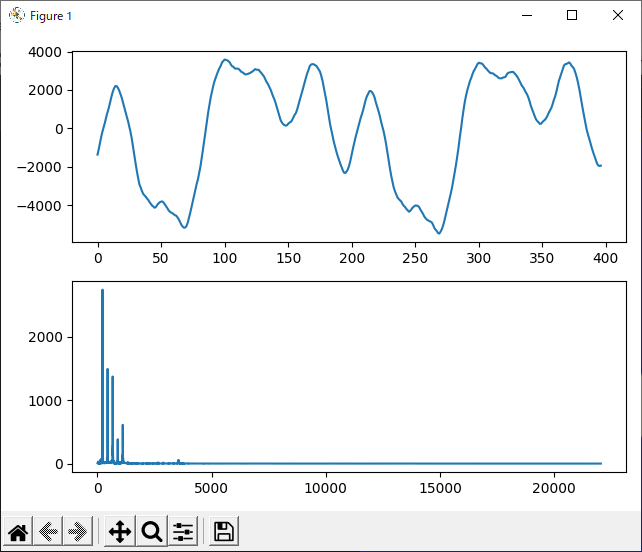
あ
まず『あ』です。基本周波数~第5高調波まで、全部で5つのピークが見えます。基本周波数以外の成分が比較的多めなため複雑な波形をしています。
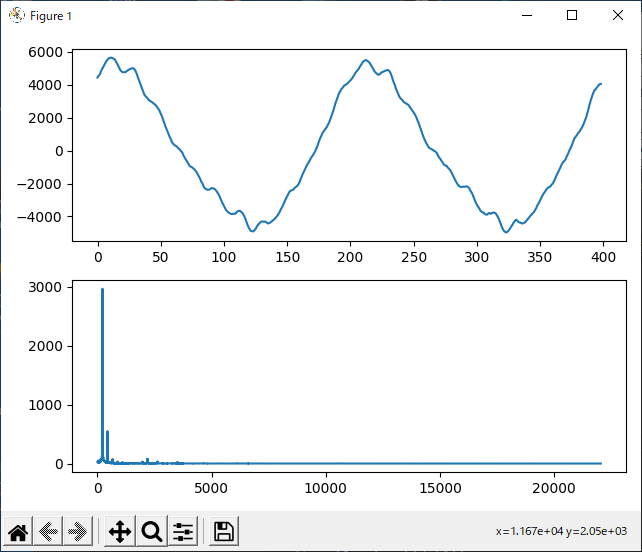
い
『い』です。基本周波数が圧倒的に多く、次に第2高調波です。第3高調波以上はほとんど見えません。
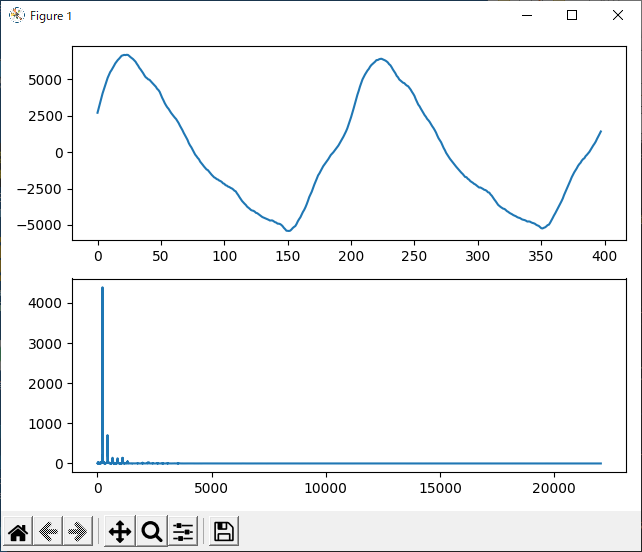
う
『う』です。『い』と似ていますが、『い』よりも高調波が少し多いです。
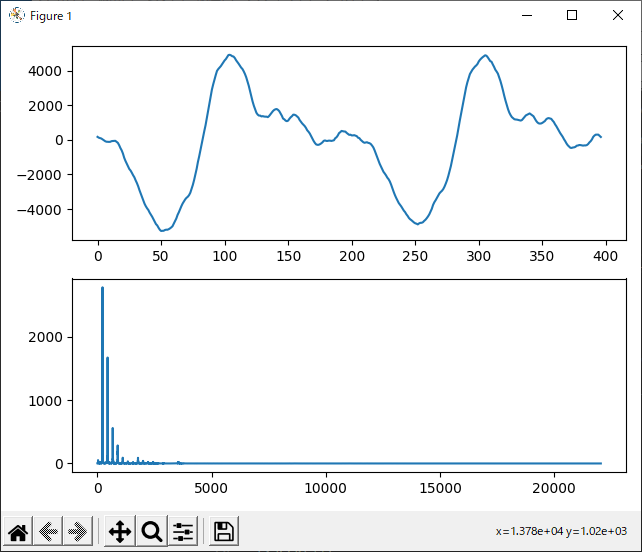
え
『え』です。『あ』の次に高調波が多いです。
お
『お』です。『あ』や『え』よりさらに高調波成分が多く、第2高調波が基本周波数と同じくらいの振幅になっています。
お次は合成してみる
次に、分析結果と同じ比率でsin波を合成して、『あ・い・う・え・お』にきこえるか実験してみます。
振幅上位5位までの成分を合成してみました。
う、うん、そう思って聞けば『あ・い・う・え・お』にきこえないこともない…かな…?
もちろんボーカロイドなどのほうがずっと聞き取りやすい発音ですが、あちらはサンプリングした人間の音声データを使って発声しています。こちらは、人間の声はデータ分析用にしか使わず、音そのものはsin波だけを素材にして合成しているという点が大きな特徴です。
今回はあり合わせの機材で自分の声を録音して実験したのですが、もっとよい環境で、発音・発声のいい人の声で(声楽の訓練を受けた人のように、一定の音程・声量で声を出せるとたぶんキレイなデータが取れると思います)実験したら、もっと面白い結果が得られるかもしれません。


コメント